Random forest (隨機森林演算法)
2021/09/06
其實這篇應該要在Cubist之前講的,但是我太想知道Cubist了,所以先研究了Cubist迴歸樹。隨機森林 (Random forest) 也是奠基於決策樹 (decision tree) 模型的一種演算法,如果不曉得決策樹是什麼可以去讀Cubist迴歸樹的內容。
隨機森林也是一個相當常使用的演算法,我也預計在碩士論文中使用 (還是樹模型用一個就好了啊?算了等結果出來再看看),因此也以一篇網誌來研究。
The difference between ordinary and extraordinary is that little extra.
—Jimmy Johnson
從樹到森林
在講解決策樹的時候,我提過決策樹有一個很大的缺點就是會因為某些outlier而有過度適配 (over-fitting) 的問題,這件事情可以用圖像化的方式來表示,假如現在的樣品要區分成兩群,如圖1 (a) 的情況我想一般的演算法都有辦法適配出一條合適的線來區隔,但圖1 (b) 的情況就有些複雜,我只改動了兩個點,但若參數沒調整好就可能因為兩個點而壞了整個分群效果,明明看到的趨勢是很明顯的兩群,卻被硬是切割成不規則的圖形。
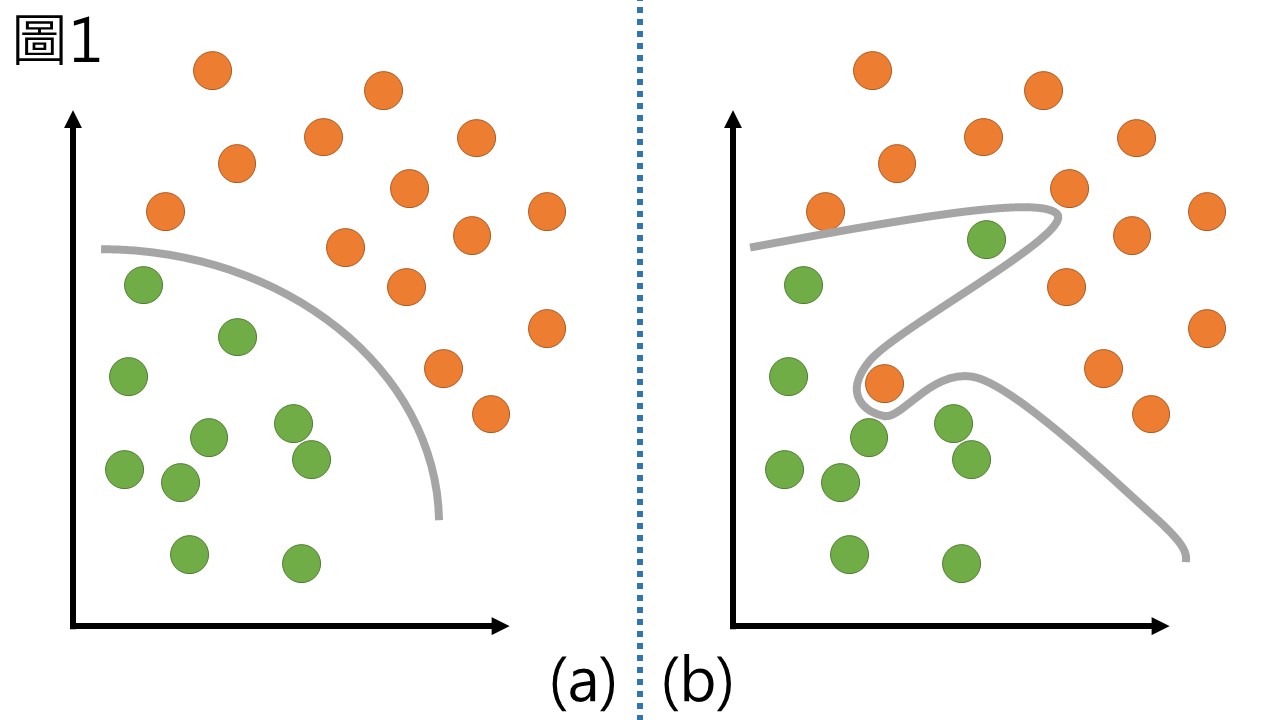
許多的演算法針對過度適配的問題作改良,而成為了優秀的演算法,隨機森林就是其中一個,他的概念從許多的演進而來,最後集大成為隨機森林,現在介紹促成隨機森林的各種進步。
Bootstrap
拔靴 (Bootstrap) 的辭源來自美國諺語”Pull yourself up by your bootstraps.”,代表靠自己的努力成功,其中的Boots就是靴子的意思,整句字面上是從自己的靴子腳印中把自己拔起來。
所謂的Bootstrap方法,是指從樣品中可重複選取的抽樣 (sample of the data taken with replacement),假設母集合有甲乙丙丁戊,抽取五個樣本時,抽到甲之後仍然可以抽到甲,因此樣本可能為甲乙丁甲戊、乙乙丙丁甲、…,Bootstrap抽樣會抽取和原本一樣多的數目,因此有些樣本會被重複抽樣。而未被選取到的樣本就被稱作out-of-bag樣本,有時會將out-of-bag樣本拿來作驗證 (validation) 使用。
由於這種方法有機會迴避掉那些離群值,較為”正常”的數值被抽到的機率會比較高,重複Bootstrap方法可以重新給予樣本一個公平的機會。
Bagging
Bagging是bootstrap aggregation的縮寫,想法相當單純,即以Bootstrap進行取樣,再針對該取樣的樣品們進行訓練而得到一個模型。也就是說Bagging可以有機會利用Bootstrap來迴避掉離群值,可以有效降低變異 (variance)。
如果一次的結果不好,那就多做幾次的概念,重複的以Bootstrap取樣會讓多數的模型都是以最為穩定的數據來進行訓練,只有少數抽到離群值的才有可能發生問題,而且Bagging可以用在任何的演算法上,這使Bagging成為演算法的新寵兒。以Bagging搭配決策樹方法就成為了一種很強大的演算法,以此再更加改良就成為了隨機森林。
隨機產生的森林
雖然Bagging搭配決策樹是一個有效的演算法,但仍有一些問題存在,例如Bagging所提取的樣本其實並不是完全獨立,有很大的機率會抽到一樣的,在這樣的情況下,有些Bagging出來的樹其實會長的差不多,這使得每棵樹雖然不完全一樣,但也只是大同小異。為了改良這個缺點,許多人嘗試為模型添加一些隨機性,讓抽樣的效果更好,最後由Leo Breiman在2001年提出的Random Forests一文中描述了這個目前已被引用接近八萬次的隨機森林演算法。
森林代表的就是很多棵樹,每棵決策樹都是根據一組Bagging樣本產生,而聚集很多棵樹就成為森林,隨機森林的隨機是在於其對Bagging所選取的變數數目添加了隨機性。假設現在有一個P維 (P個特徵) 的資料,隨機森林演算法的計算方法可以表示成這樣:
- 給定要建立的模型 (樹) 數量m
- 對於每棵樹都利用Bagging來選取樣本,因此樣本數皆和原本的一致
- 對於樹的節點選取,只以P個特徵中隨機挑k個來比較分割效果,並以不純度指標衡量此分割是否有效,保留最有效的分割方式
- 重複第3點直到無法再分割或是無法再降低不純度,形成m棵樹 (不進行修剪pruning)
- 最終的預測結果是m棵樹投票的多數決
所以白話一點來說,其實隨機森林是很多個決策樹所組成,但 (1) 訓練的樣本是由Bagging產生 (2) 選取節點時,只會從k個特徵中挑選,並不會把所有特徵都拿來比較。
當中的k值常被稱作mtry,在原本的論文中建議把k值設為P/3左右的數值,而在Applied Predictive Modeling中則是建議從2到P之間,均勻的取5個數值,再觀察效果,模型數量m則建議超過1000個。由於每次只要比較k個特徵,所以隨機森林的計算會比單純的決策樹快。
隨機森林克服了過度適配的問題,成為比決策樹更加優秀的監督式學習演算法,我打算在碩士論文中使用看看,到時有心得會再更新。
參考資料
Applied Predictive Modeling
Breiman, L. 2001. Random Forests. Machine Learning, 45, 5–32. https://doi.org/10.1023/A:1010933404324