Home | About | Posts | English

Principal component analysis, PCA (主成分分析)

2021/09/04
在此宣布網誌進入大統計時代！
終於也到了這個我最期待的單元了，主成分分析是一個環境科學上相當常用，但入門難度相對高的統計方法，我們實驗室的新學生很常都在主成分分析上碰到瓶頸，這幾天我在教別人主成分分析，因此起了這個念頭，再次整理一下主成分分析的原理。這篇文章不會包含程式碼，我會先介紹主成分分析大致上的應用方式、原理，最後才會講到其數學的算法，那就開始吧！

Time goes on. So whatever you’re going to do, do it. Do it now. Don’t wait.
—Robert De Niro

何謂PCA

主成分分析 (principal component analysis, PCA) 是一種降維度 (dimensionality reduction) 的演算法，因此我們可以先從降維度這個詞開始講起。維度 (dimension) 代表我們用於表示一個座標點所需要用的參數數目，舉例來說，我們常見的XY散布圖就是由兩個維度 (X跟Y) 所組成的平面，一個維度就是一條線，兩個維度組成一個面，三個維度則可以組成立體空間。物理學上，我們是生活在一個三維空間中，還有一個單向的第四維是時間。

有了維度的概念，就可以看到我們平時處理的資料，例如我們要測量土壤的八大重金屬，這代表每一個樣品我們都測量了八個項目，也就是說這組資料有八個維度，但由於八個維度太難編資料了，把情況換成學生的考試成績。假設現在每個學生都考了三門期末考，期末考的科目包含數學、科學還有英文，然後有6位學生參加考試，那麼虛構的考試結果可能如下：

Student Math Science English
Andy 98 97 52
Bob 48 58 90
Caleb 44 65 99
David 92 96 63
Ethan 42 57 86
Frank 70 80 70

這個數據是一個三維度的資料，那麼此時，我們能從這組資料裡看出什麼呢？要回答這個問題，繪圖是最好的方法，也許數字沒有什麼感覺，但在科學上圖表是非常有感覺的，把同學的成績繪製成三維的圖：

從圖中就可以看到，其實同學成績的分布是有一個規律的，英文成績越高的學生 (Bob、Caleb和Ethan)，他們的數學跟科學都考比較差，相反的數學跟科學成績較高的學生 (Andy及David)，他們的英文成績較差，而Frank則是介於中間。如果我們把學生用”理科傾向”來衡量，理科傾向越高的學生，就會在數學與科學上表現較好 (但英文較差)，理科傾向越低的學生，則是在數學及科學表現不佳 (但在英文表現較好)，至此我們成功的用一個維度 (理科傾向) 來表示原本三個維度 (數學、科學、英文) 才能表達的事情。

降維度的功能，就是讓多維度的資料可以用更簡單的方法來表示，那麼問題來了，我們要怎麼描述這件事情？亦或者是，當維度提高到變成八大重金屬，無法繪圖的狀況下，我們怎麼看出這種隱藏的維度？
此時就是PCA派上用場的時候了，降維度即是讓多維度的資料可以更為容易的理清，不同的降維度方法有各自的原理，而PCA的原理就是保留最大的變異，並且用比較少的座標代表較多的資料。

PCA：保留最大的變異

這裡會開始進入有點數學的地方，但我選擇用最簡單的解釋方法，只要會看圖就能了解，也可以去看StatQuest的影片，我覺得他的解釋很容易理解。
假設我們現在處理的是二維的資料，分為X1軸與X2軸，先將其調整到原點是所有數據的平均值，如圖1。

如果要像上一段一樣找一個維度來代表這組數據，我猜大多數人直覺會選的都是一條傾斜45度的直線，但為什麼？原因是這條線可以保留最大的變異。
若我們有一組資料如圖1，那麼這組資料會有它的分散程度，也就是其變異 (variation)，變異是把點座標投影到維度上之後，和平均值的差距 (圖2)，在資料科學上這種變異其實就是你的資訊量，有的數值距離平均相當遠，表示他具有較多的資訊，有些數值距離平均很近，可能就沒什麼資訊，在土壤科學上也是，距離平均值越遠的數值可能越有其重要性。

那如果要找一個新的座標軸來代表這組數據，我們就會希望新的座標軸可以盡可能的保存資訊，也就是讓變異越多越好，變異越多就更能夠區分樣品間的不同，這裡示範兩種不同座標軸所能保留的變異 (圖3)，對於圖中的紅點來講，可以很明顯的看出軸1保留最多的變異，使用主成分分析的目的就是找到一個保留最多變異的新座標軸，該座標軸就稱作第一主成分 (PC1)。

接著，該如何找到保留最高變異的新座標軸？我們用假想的一個軸P來表示，計算所有點投影到軸P上的變異值並且將其平方相加 (SS, sum of squares)，這樣就是代表新座標軸所能夠保存的變異 (圖4)。

在計算各條軸所能得到的SS值之後，找到一條其SS值最大的座標軸，這條座標軸就被叫做第一主成分 (principal component 1, PC1)，PC1是一條能夠保存最多變異的座標軸，接著以與PC1正交為原則，我們再計算SS值最大的另一個座標軸，就做為第二主成分 (PC2)，而在這個假想的二維座標中，和PC1正交的直線只有一條，因此該條直線就是PC2 (圖5)，但如果我們的變數超過兩個，選取主成分的時候就要考慮所有的座標軸，也是因為主成分分析要求每一個主成分互相正交，且投入幾個變數就能算出幾個主成分。

以上，PC1計算完畢，需要找一個方法來表示PC1，表示的方法就是將PC表示成X1與X2的線性組合 (linear combination)，也就是\(PC1 = k_1 X_1 + k_2 X_2\)這種方法。由於每條線都可以用一個單位向量來表示，X1與X2各自有其單位向量，如圖6棕色的X1與X2，這兩個單位向量可以透過組合來表示PC1的單位向量 (圖6的紅色向量)，PC1的單位向量就被稱作PC1的eigenvector (特徵向量)。

而PC1的eigenvector可以表示為k1倍的X1向量加上k2倍的X2向量所組成 (圖7)，而用於組成eigenvector的k1與k2，就稱作X1與X2變數的loading (變數負荷量)，loading不會超過1，當loading越高時，表示主成分和這個變數越有關。eigenvector就是由變數線性組合而成的PC1單位向量，有時候又被稱作rotation，是一樣的意思。

而我們剛剛計算的SS平方和，則是代表PC1所能保留的變異量，這個數值就被稱作PC1的eigenvalue (特徵值)，每個主成分都有自己的一個eigenvector與eigenvalue，根據Kaiser’s rule (凱莎原則)，eigenvalue大於1的主成分，通常被考慮是較好的。

計算完PC1之後，我們知道如何用線性組合表示eigenvector，並且獲得PC1的eigenvalue得以衡量PC1能保留多少的變異，接著要知道的是PC1所保留的變異占總變異的多少，總變異就是把所有PC的eigenvalue相加，我們把PC1的eigenvalue除以總合的eigenvalue，就能得到PC1所能解釋的變異百分比。

\[\begin{aligned} P&ercentage\ of\ variance\ explained\ by\ PC1\\ &= \frac{(eigenvalue\ of\ PC1)}{(eigenvalue\ of\ PC1) + (eigenvalue\ of\ PC2)+ (eigenvalue\ of\ PC3)+....} \end{aligned}\]

我們通常會用累積的解釋變異百分比 (cumulative probability) 來表示，一般來說若前兩個主成分可以解釋超過70%的變異，那麼這個主成分分析就被視為是不錯的。
最後，我們會希望看到樣品點投影到新座標軸上的位置，在前面的圖5中，PC1及PC2成為了新的座標軸，用這個新的座標系統所表示的點座標，就被稱為各點在PC1上的score。至此我們已經完成了最基礎的PCA教學，只要確保自己了解底下的這些名詞，就算不會計算PCA也能用程式跑出來，能夠解釋即可。

數學的PCA

這部分就是真的數學了，沒興趣的人可以不用繼續看，畢竟學會手算PCA其實一點用也沒有，不如去看我寫的R教學。
前面我們將PCA表示成線性組合，線性組合又可以將其擴大寫成矩陣的方式，我們將其表示如下：

\[\begin{aligned} PC1 &= k_1 X_1 + k_2 X_2 + k_3 X_3 + ... + k_n X_n\\ &= \begin{bmatrix}k_1\\k_2\\...\\k_n\end{bmatrix} \begin{bmatrix}X_1&X_2&...&X_n\end{bmatrix} \\ &= \overrightarrow{k} \overrightarrow{X} \end{aligned}\]

其中的矩陣k就是eigenvector，要如何求取這個線性組合k矩陣所能保留的變異數？我們要使用變異-共變異矩陣S。

\[S = \begin{bmatrix}Var(X_1)&Cov(X_2,X_1)&...&Cov(X_n,X_1)\\Cov(X_1,X_2)&Var(X_2)& &Cov(X_n,X_2)\\...& & &...\\Cov(X_1,X_n)&Cov(X_2,X_n)&...&Var(X_n)\end{bmatrix}\]

一個線性組合k所能夠保留的變異數λ，計算方式如下 (可以自己算算看，真的是這樣)：

\[\begin{aligned} \lambda &= k'Sk\\ &= \begin{bmatrix}k_1&k_2&...&k_n\end{bmatrix} \begin{bmatrix}Var(X_1)&Cov(X_2,X_1)&...&Cov(X_n,X_1)\\Cov(X_1,X_2)&Var(X_2)&...&Cov(X_n,X_2)\\...&...& &...\\Cov(X_1,X_n)&Cov(X_2,X_n)&...&Var(X_n)\end{bmatrix} \begin{bmatrix}k_1\\k_2\\...\\k_n\end{bmatrix} \end{aligned}\]

我們要求λ最大時的線性組合k，方法是在線性代數中求取eigenvalue的方法

\[\begin{vmatrix}S-\lambda I\end{vmatrix} =0\]

求取使上式為0的λ即為eigenvalue，把eigenvalue代回下式

\[\begin{aligned} \lambda &= k'Sk\\ \lambda k &= Sk \end{aligned}\]

這樣子就可以算得線性組合k，也就是eigenvector，這樣就完成PC1的運算了。要計算PC2的方法是增加一條限制，那就是PC2的eigenvector必須和PC1的eigenvector正交，在每個主成分都正交的條件下，我們可以計算出所有的主成分。

其他東西

Scree plot (陡坡圖)
陡坡圖是繪製eigenvalue的圖，將主成分的eigenvalue繪圖表示，eigenvalue越高表示主成分能解釋的變異越多，而eigenvalue必定會遞減，所以會是陡坡的圖形。
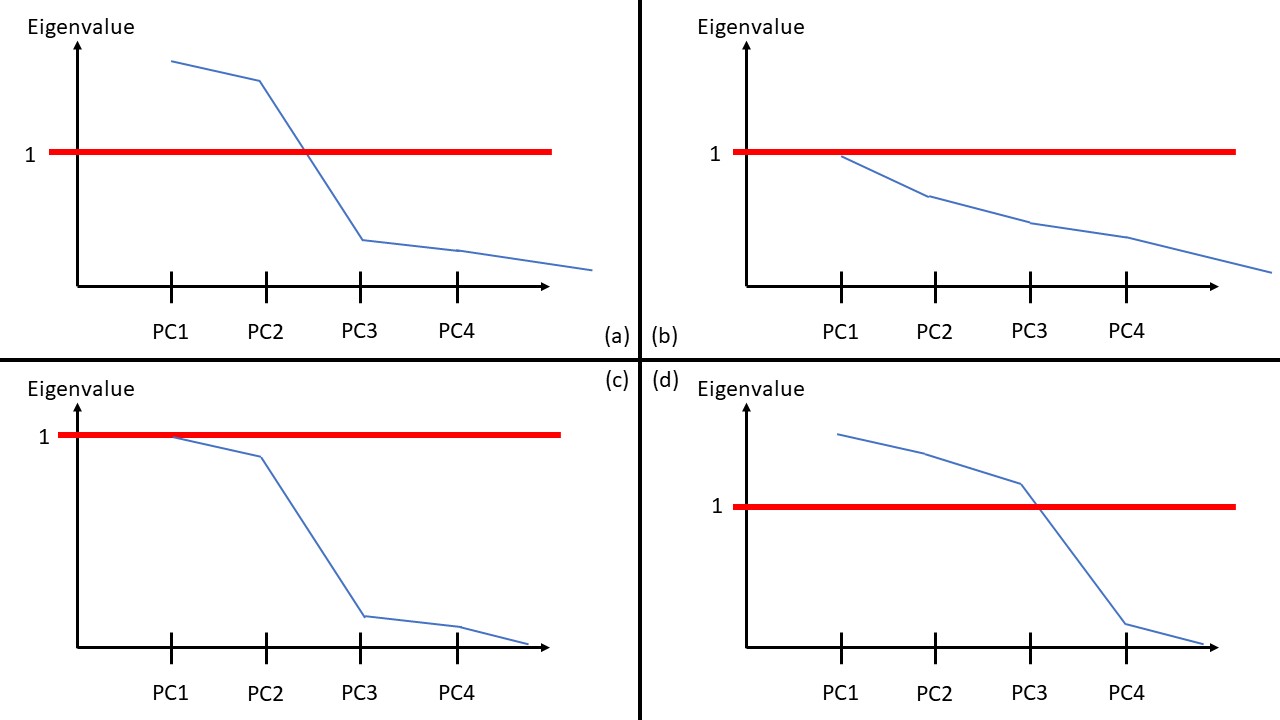
陡坡圖中eigenvalue大於1的主成分可以選取，而若陡坡降的越快，就表示前幾個主成分能解釋的變異很多，效果也越好，如下圖 (a) 是一個很經典的陡坡圖，有兩個PC的eigenvalue超過1，且PC2之後的eigen也快速下降，這代表PC1跟PC2的降維效果是很成功的；圖 (b) 裡面每個eigenvalue都很低，且都沒有超過1，這樣的主成分分析效果可能就不太好；圖 (c) 雖然和圖 (a) 很像，但圖 (c) 裡的eigenvalue都小於1，可能效果也不好；圖 (d) 則是在PC3之後才開始下降，這代表PC3可能也是一個重要的因素，需要看看PC3的loading再決定。

總而言之，PCA的概念雖然能解釋，但有很多實際操作才能理解的眉角，在獲得資料之後，不妨嘗試看看使用PCA吧，我很推薦使用R語言進行PCA。