Principal component analysis (PCA) 的R實作
2021/09/04
這篇建議搭配主成分分析一起服用。
用R跑PCA相當的容易,容易到很多人不懂PCA卻也弄得出來,但建議還是要先理解PCA的原理才開始使用,R筆記也是一個很棒的參考點。
用R寫PCA
首先我使用在主成分分析文章中使用的學生資料做示範,表格如下:
| Student | Math | Science | English |
|---|---|---|---|
| Andy | 98 | 97 | 52 |
| Bob | 48 | 58 | 90 |
| Caleb | 44 | 65 | 99 |
| David | 92 | 96 | 63 |
| Ethan | 42 | 57 | 86 |
| Frank | 70 | 80 | 70 |
將數據輸入R
dat <- data.frame(matrix(c(98,97,52,48,58,90,44,65,99,92,96,63,42,57,86,70,80,70), nrow=6, ncol=3, byrow = T))
row.names(dat) <- c("Andy","Bob","Caleb","David","Ethan","Frank")
colnames(dat) <- c("Math", "Science", "English")
接著要使用的函數名為prcomp,即是principal component的意思,他所需要的參數有三個,分別為formula、data與scale。
formula代表要使用哪些變數資料做主成分分析,使用三個科目表示
formula = ~ Math+Science+English;data則是資料的名字,scale是True or False,輸入T代表數據會經過標準化 (減去平均再除以標準差),強烈建議需要標準化資料,因為有些變數的範圍差距很大,會影響結果。
pca <- prcomp(formula = ~ Math+Science+English,
data = dat,
scale = T)
pca
若變數很多不想一個一個打字的話,提供可以使用paste(colnames(dat),collapse = "+")這行指令。
至此,我們的主成分分析已經完成 (這麼快!?)
所有需要的數據都存在pca這個資料裡,應該會顯示下面這樣
Standard deviations (1, .., p=3):
[1] 1.70179452 0.30930959 0.09068076
Rotation (n x k) = (3 x 3):
PC1 PC2 PC3
Math -0.5854414 0.1504653 0.7966295
Science -0.5762037 0.6140123 -0.5394240
English 0.5703049 0.7748220 0.2727695
所謂的rotation就是變數的負荷量 (loading),依照我的習慣,我會先看主成分分析的eigenvalue與累積解釋變異。
vars <- (pca$sdev)^2 # 提取特徵值
props <- vars / sum(vars) # 提取解釋比例
cumulative.props <- cumsum(props) # 提取累積比例
vars # 呼叫特徵值
cumulative.props # 呼叫累積比例
提取出來的vars就是eigenvalue,cumulative.props就是累積的解釋變異,輸出的結果應該如下:
> vars
[1] 2.89610458 0.09567243 0.00822300
> cumulative.props
[1] 0.9653682 0.9972590 1.0000000
我們可以看到PC1的eigenvalue有2.896,但PC2的eigenvalue只有0.096,根據Kaiser’s rule (凱莎原則),eigenvalue > 1的主成分較好,而在累積解釋比例的部分,PC1就能解釋97%的變異,可以說是相當好 (因為數字是我調過的,現實哪有這麼好的事情)。
確定PC1的效果很好之後,下一步要做的就是取出各變數的loading,這步驟使用pca$rotation,從pca資料抽取出rotation (也就是loading)。
> pca$rotation
PC1 PC2 PC3
Math -0.5854414 0.1504653 0.7966295
Science -0.5762037 0.6140123 -0.5394240
English 0.5703049 0.7748220 0.2727695
結果如上,PC1中數學與科學的loading都是負的,而英文則是正的,這跟我們在主成分分析文章中發現的一樣,有隱藏的變數 (理組傾向),當理組傾向越高時數學跟自然的成績越好,英文成績越差,而PC1就將這個傾向表現出來。另外,loading的正負號僅表示不同變數之間的相對性,其絕對值越大才是代表影響越大。
PCA的結果呈現上,第一個會表示其累積百分比,再來是變數loading,最後一個則是score plot,這三個都呈現出來,你的PCA才完整,現在要來繪製score plot。
由於繪圖多只能繪製二維圖,所以通常會挑選前兩個主成分 (PC1及PC2) 來繪圖,但如果其他的很有趣當然也可以畫。要將score提取出來,使用pca$x來提取各樣本 (學生) 數據在投影到PC1後的score。
> pca$x
PC1 PC2 PC3
Andy -2.2254737 -0.1477052 0.02261740
Bob 1.3932171 -0.1193047 0.15567019
Caleb 1.5526425 0.4817224 -0.04236503
David -1.7024518 0.2583078 0.02778427
Ethan 1.4385213 -0.3623239 -0.06764923
Frank -0.4564554 -0.1106965 -0.09605761
將前面兩個PC繪圖表示,推薦使用套件函數autoplot可以快速畫出能看的圖 (當然要美觀還是要細調,但這已經能看了),需要下載套件ggplot2與ggfortify。
library(ggplot2)
library(ggfortify)
autoplot(pca, data = dat,
size=2,
x=1, y=2,
scale=F)+
geom_text(vjust=-1, label=rownames(dat), cex=4)
接著應該就會看見下面這張圖
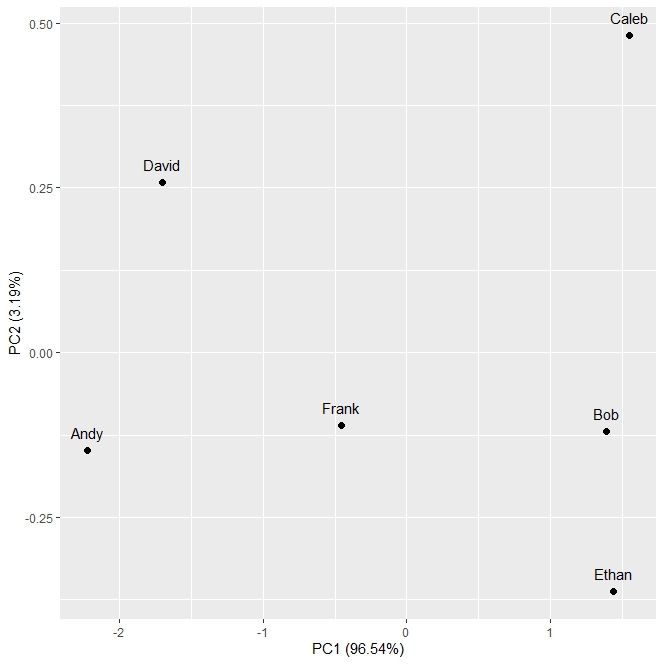
在PC1上面,落在右邊的三個人 (Bob、Caleb和Ethan) 是屬於理科傾向較低,英文考較好的學生,反之另一邊的兩個人 (Andy及David) 則是理科傾向較高,數學與科學考較好的學生,PCA就能如此揭露隱藏在數據後面的另一個維度。
最後的叮嚀
雖然PCA很強大,但仍有一些需要注意的地方。
- 資料的共線性:之前在迴歸分析裡面說過,資料的共線性會是一個問題,這放到PCA裡來說,PCA可以是個解法,當你的數據共線性很多的話,PCA的效果通常會很好,因為他們都被相同的因素控制,所以也能很容易的抓出主成分,你再使用主成分去進行迴歸分析,就可以避免掉共線性的問題了。
- 標準化:數據一定要標準化,假如我們處理的是一個大數值的變數 (如土壤質地,差距可能是10和50),和一個小數值的變數 (如土壤pH,差距可能是4.3和4.8),這樣的差異會影響PCA的結果,因此建議都要使用標準化。
- PC1到底是什麼:很遺憾,沒有辦法可以明確的告訴你PC1到底是什麼,我們只能說他是一個能保留最大變異的座標軸,一個隱藏的維度,只能依靠與資料有關的經驗 (領域內的專業知識),來推測PC1可能是什麼,觀察有關的loading以及score,進而做出合理的結論。
- 哪些點可以圈在一起:有些PCA score plot中會把相近的點圈在一起,這個圈法有沒有特定規律?老實說可以自己圈,如果沒有特別寫方法的話可能都是自己任意圈的,因為解釋是主觀的。如果要用統計方法圈出相近的點,則可以考慮分群方法例如k-means。
其他能夠參考繪圖的網站:
https://cran.r-project.org/web/packages/ggfortify/vignettes/plot_pca.html
https://stackoverflow.com/questions/40223219/autoplot-how-to-adjust-loading-labels
更新:我又寫了另一篇PCA的R教學歡迎去看。