學生實驗-土壤質地分析 (Determination of Soil Texture)
2021/10/12
又到了每年準備學生實驗的日子了,我們實驗室的碩班都需要帶實驗,藥品與寫黑板的內容需要由各班助教準備,這次我又是拿到週一上午的農化班,因此第一個實驗就會是由我來準備。
這次因為疫情的關係,前三週都不會到校上課,所以第四週的土壤質地測定就是學生的第一週實驗,提早一週準備是一個好習慣。
Mesh number
風乾磨碎過篩時通過的標準篩網有國際標準,其單位篩目 (mesh) 指的是一寸 (inch) 內有幾個格子,例如常用的10 mesh就代表1 inch約被分成十個等分,能通過的就視為直徑2 mm以下的土壤。同理100 mesh代表1 inch被分成100個等分。
要注意的是mesh並不是精確的單位,由於定義是一寸裡面分幾個,但是篩網的網目是金屬有粗細的,所以並不能精確的把10 mesh代表為2 mm,頂多只能作為一個估計,然而10 mesh被土壤學界廣泛接受,所以寫文章時只需描述使用的是10 mesh標準篩即可。
Soil texture
能通過10 mesh標準篩網的即可視為土壤,而土壤質地分析則是用於測定土壤中無機粒子的大小組成,可分為砂粒 (sand)、坋粒 (silt) 與黏粒 (clay),他們的大小關係如下。
| Type | 砂粒 (Sand) | 坋粒 (Silt) | 黏粒 (Clay) |
|---|---|---|---|
| Size (mm) | 2 mm - 0.05 mm | 0.05 mm - 0.002 mm | <0.002 mm |
| Size (µm) | 2000 µm - 50 µm | 50 µm - 2 µm | <2 µm |
測定土壤質地得以知道土壤的風化過程、水流的速度、營養素吸附的程度等很多不同的特性,對決定土壤利用至關重要。要測定土壤質地可能有人會想用篩網就好,但是其實土壤中的有機質會影響到土壤的膠結,也就是說直接篩的話有的粒子會黏在一起,所以通常會用沉降法 (sedimentation method) 來測定。
有兩種常見的沉降法,分別為比重計法 (hydrometer method) 與吸管法 (pipette method),後者因為具有較複雜的前處理過程,所以結果較為準確,研究多採用吸管法,但比重計因為比較快速,也有其適用的地方例如農業的快速評估,學生實驗只會帶到比重計法,所以這篇文章只會講解到比重計的部分。
來點物理
沉降法所使用的原理為Stokes’ law,如果對物理沒興趣的人,這部分只要記住粒子在水中沉降的速度與其半徑平方成正比就好,也就是越大的粒子沉降越快,以此原理即可區分不同粒子大小。
對物理有興趣的人,Stokes’ Law的方程式有四項基本假設:
- 粒子沉降時迅速達到終端速度
- 在水中僅重力、浮力與黏滯性三種作用
- 粒子是圓的
- 粒子之間互相不作用
很明顯的現實情況會跟基本假設有點不同,這就是誤差的來源。
在液體中粒子的沉降受到重力與浮力影響,一個半徑為r的球體其體積為\(\frac{4}{3}\pi(\frac{(2r)^3}{8})\),粒子密度為\(d_p\ (g\ cm^{-3})\),液體密度為\(d_m\ (g\ cm^{-3})\),重力加速度\(g\ (cm\ s^{-1})\),根據一些高中物理,重力為體積乘以密度乘以重力加速度,浮力則為排開液體的體積乘以密度乘以重力加速度 (方向與重力相反),因此整合起來重力-浮力為
\(\begin{aligned}
F_{down}&=\frac{4}{3}\pi(\frac{(2r)^3}{8})(d_p-d_m)g \\
&=\frac{4}{3}\pi r^3(d_p-d_m)g
\end{aligned}\)
再來,在達到終端速度時,粒子所受到的黏滯性也會與受力相等,令黏滯性係數為\(\eta\ (mPa\cdot s)\),則方向向上的黏滯力與終端速度\(V (cm\ s^{-1})\) 的關係為
\(F_{up}=3\pi (2r) \eta V\)
因此,把向上的力與向下的力畫上等號並且約分可得
\(\begin{aligned}
F_{down}&=F_{up}\\
\frac{4}{3}\pi r^3(d_p-d_m)g &=3\pi (2r) \eta V\\
2r^2(d_p-d_m)g &= 9\eta V\\
\end{aligned}\)
接著繼續讓左邊只留下終端速度V,並且將常數彙整得到
\(\begin{aligned}
V &= \frac{2gr^2 (d_p-d_m)}{9\eta}\\
&= kr^2
\end{aligned}\)
如上式,終端速度V只跟半徑平方成正比,其餘都是固定的常數,因此在沉降過程中半徑越大的粒子沉降速度越快,可由此區分不同粒徑大小,這即是Stokes’ law原理。
接下來進一步,我們要估算粒子沉降的時間,假設時間內下降了高度\(h\ (cm)\),令速度為高度h除以時間t,可進一步換算
\(\begin{aligned}
V &= \frac{2gr^2 (d_p-d_m)}{9\eta}\\
\frac{h}{t} &= \frac{2gr^2 (d_p-d_m)}{9\eta}\\
t &= \frac{9\eta h}{2gr^2 (d_p-d_m)}
\end{aligned}\)
為了後續運算的方便性再進一步改寫為
\(\begin{aligned}
4r^2 &= \frac{18\eta h}{g (d_p-d_m)t}\\
2r &= \sqrt{\frac{18\eta h}{g (d_p-d_m)t}}
\end{aligned}\)
這個原理會在後面進一步用到
比重計法
比重計 (hydrometer) 是一個組成固定的玻璃儀器,由一根長長的管狀部分與球狀 (bulb) 部分組成,管狀部分最上部有一個零點,零點往下會有讀數R,由讀數R到球狀部分的長度為\(L_1\),球狀部分則為長度\(L_2\),而球狀部分體積\(V_B\),使用時將比重計垂直放入水中即可讀取數值。
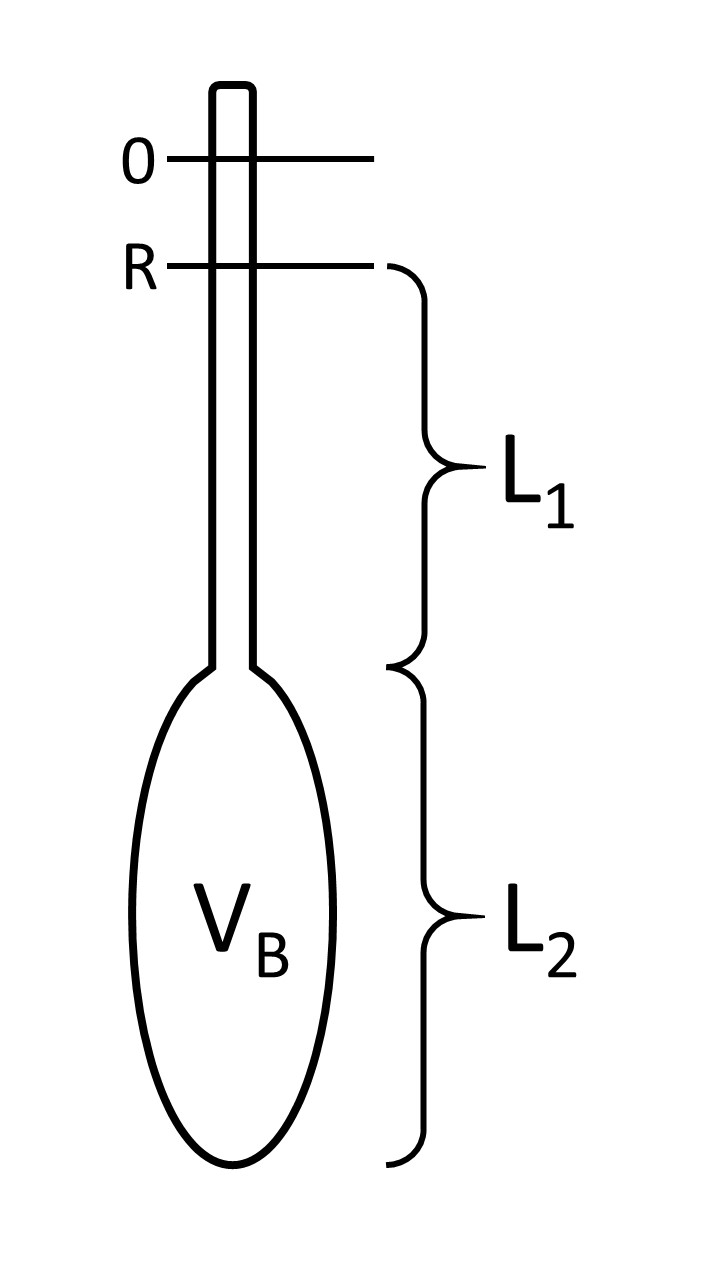
來介紹他的物理,延續上一個部分的算式,可以將常數化簡得到
\(\begin{aligned}
2r &= \sqrt{\frac{18\eta h}{g (d_p-d_m)t}}\\
2r &= \theta t^{-1/2}
\end{aligned}\)
因此\(\theta = \sqrt{\frac{18\eta h}{g (d_p-d_m)}}\),其中唯一不知道的數值\(h\)為比重計下降的有效深度,根據比重計本身的設計,\(h\)會滿足\(h = L_1 + 0.5(L_2 - V_B / A)\),其中A是沉降筒的底面積。
根據以上的數值,可以換算讀數R所對應到的有效深度\(h\),藉由有效深度\(h\)、溫度 (即對應的黏滯係數\(\eta\)) 與密度 \((d_p-d_m)\),即可求得\(\theta\)。
再由有效深度與\(\theta = \sqrt{\frac{18\eta h}{g (d_p-d_m)}}\)推算回粒子的密度\(d_p\)。
到這裡,已經有聰明的人將讀數R與其在固定環境中對應的\(\theta\)製表,只要利用讀數R就可以查到室溫下的\(\theta\)。有人更進一步建立讀數R與溶液中粒子濃度C的檢量線,然而要校準溶液中的粒子濃度C就需要同時有一個空白 (不含土) 的讀值\(R_L\),校準後的關係是\(C=R-R_L\),利用讀數R與前人建立的檢量線就可以計算出溶液中的土壤量。這就是為什麼我們只要將比重計的讀數除以土重,再乘以100%就可以得到比例,因為前人都幫我們算好了。
超過一定時間,砂粒就會沉降到底而不存在溶液中,當砂粒沉降完時可放入比重計測量坋粒+黏粒,再經過一定時間坋粒也會沉降到底而不存在溶液中,當砂粒與坋粒沉降完後可放入比重計測量黏粒。
我們常使用的40秒與2小時是一個估計的經驗式 (empirical model),出自Bouyoucos (1962) 所以又稱Bouyoucos method,以40秒的數值代表坋粒+黏粒,2小時的數值代表黏粒,這個方法會產生約10%的誤差,但對於質地分析而言這個準確度已經足夠了,要更好的準確度則可以使用吸管法。
參考資料
Bouyoucos, G.J. 1962. Hydrometer Method Improved for Making Particle Size Analyses of Soils1. Agronomy Journal, 54(5), 464-465. https://doi.org/10.2134/agronj1962.00021962005400050028x
Gee, G.W. and Bauder, J.W. 1986. Particle-size Analysis. In: A. Klute (Ed.), Methods of Soil Analysis: Part 1, 2nd edition. Agronomy Monograph 9. (p.p. 383-411). Madison, WI: American Society of Agronomy and Soil Science Society of America. https://doi.org/10.2136/sssabookser5.1.2ed.c15